AES 對稱式加解密法 by 陳鍾誠 | CodeData
top
技術文章 / 社交設計

AES 對稱式加解密法

分享：
閲讀次數：61432 發表時間：2013/09/23
tags: JavaScript 密碼學 密碼 AES C 語言

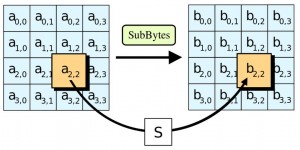
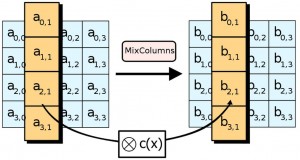
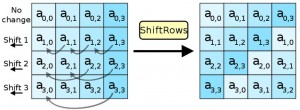
在前面兩篇文章中，我們介紹了幾個比較簡單的加解密方法，像是凱薩加密法、以及 XOR 加密法等，以下是這兩篇文章的網址：

但是、上述幾種簡單的加密法，都比較容易受到破解，現在通常已經不使用了。

在本文中，我們將介紹一個現代的高強度加解密方法，稱為 Advanced Encryption Standard (AES)，這個加解密法乃是美國政府公開徵選用來取代 DES 加密法的一種新型加密法，目前已經廣泛用於很多加密標準當中。

前言

AES 加密法的發明人是比利時的 Joan Daemen 和 Vincent Rijmen，因此當初兩人決定採用 Rijndael 這個結合兩人姓名發音的名稱，投稿到「美國國家標準與技術研究院」所舉辦的徵選評比當中。

後來「美國國家標準與技術研究院」決定接受 Rijndael 方案為最終標準，並選擇其中三種不同的密鑰長度做為標準，分別是 128、192 與　256位元的版本。

相對於較為老舊的 DES 加密法，AES 由於採用了「置換-組合架構」，因此在「軟體及硬體」上都可以快速的加解密，不像 DES 只能在「硬體」上快速的加解密，在純軟體實作上的速度會過慢。

AES 已經被 SSL 加密標準納入採用，像是 OpenSSL 這個開放原始碼的 SSL 實作就有用 AES 加解密的程式碼，在本文中，我們將透過 AES 瞭解新一代的加解密方法。

原理

AES 的原理，是在一個稱為 state 的 4*4 Byte 矩陣上運作，大致上包含了四個主要的步驟，如下所示：

1. AddRoundKey ：資料與金鑰做 XOR 運算，也就是 b[i,j] = a[i,j] xor k[i,j]。
2. SubBytes ：透過 S-Box 函數 S 將每個 Byte 做轉換，也就是 b[i,j] = S( a[i,j] )。
3. ShiftRows ：對於矩陣的每一橫列進行 Shift 移位的動作，移位的步伐大小與列號成正比。
4. MixColumns ：對於矩陣的每一直行，與一個多項式 c(x) 進行多項式乘法。

以下是這些操作的示意圖，請讀者參考。

AES-AddRoundKey
圖、AES：AddRoundKey 步驟示意圖

AES-SubBytes
圖、AES：AES-SubBytes 步驟示意圖

AES-MixColumns
圖、AES：AddMixColumns 步驟示意圖

AES-ShiftRows
圖、AES：AES-ShiftRows 步驟示意圖

AES 加解密演算法

AES 的加密與解密，都需要進行金鑰展開的 KeyExpansion() 動作，如下函數所示，然後再用展開後的金鑰去進行加解密的算法。

以下是加密動作的演算法：

(1). 對第一個區塊，進行下列動作
   	1. AddRoundKey()
(2). 從第二個區塊開始，對每個區塊都執行下列動作
   	1. SubBytes()
   	2. ShiftRows()
   	3. MixColumns()
   	4. AddRoundKey()
(3). 對最後一個區塊，執行下列動作
   	1. SubBytes()
   	2. ShiftRows()
   	3. AddRoundKey()

您可以注意到上述四大步驟在整個演算法中，執行的次數並不是一樣多的，AddRoundKey() 函數在第一輪與最終輪都有執行，但是最終輪卻沒有執行 MixColumns() 的動作。

相反的，AES 解密的演算法，則是在第一輪執行三個步驟，而在最後一輪只執行一個步驟，如以下所示：

以下是解密動作的演算法：

(1). 對最後一個區塊，進行下列動作
   	1. AddRoundKey()
   	2. ShiftRows()
   	3. SubBytes()
(2). 從倒數第二個區塊開始，對每個區塊都執行下列動作
   	4. AddRoundKey()
   	3. MixColumns()
   	2. ShiftRows()
   	1. SubBytes()
(3). 對第一個區塊，執行下列動作
   	1. AddRoundKey()

您可以看到在 AES 的加解密過程中，加密時採用正向的進行掃描，而解密時卻是逆向的進行掃描，這是相當有意思的一點。

原始碼實作

為了理解 AES 的原理與程式寫法，我們找了一個非常簡單的 AES 實作，JSAES 是一個採用 javascript 實作的 AES 開放原始碼函式庫，您可以從下列網站下載。

然後、由於本系列文章是採用 C 語言實作的，因此筆者將原本用 JavaScript 實作的 JSAES，翻譯修改為 C 語言的版本，原始碼如下所示。

// 本程式由陳鍾誠將 jsaes: AES in JavaScript (作者： B. Poettering) 翻譯為 C 語言版，
// 來源為 http://point-at-infinity.org/jsaes/，授權為 GNU GPL 授權。

#include <stdio.h>

#define BYTE unsigned char

void printBytes(BYTE b[], int len) {
  int i;
  for (i=0; i<len; i++)
    printf("%d ", b[i]);
  printf("\n");
}

/******************************************************************************/

// The following lookup tables and functions are for internal use only!
BYTE AES_Sbox[] = {99,124,119,123,242,107,111,197,48,1,103,43,254,215,171,
  118,202,130,201,125,250,89,71,240,173,212,162,175,156,164,114,192,183,253,
  147,38,54,63,247,204,52,165,229,241,113,216,49,21,4,199,35,195,24,150,5,154,
  7,18,128,226,235,39,178,117,9,131,44,26,27,110,90,160,82,59,214,179,41,227,
  47,132,83,209,0,237,32,252,177,91,106,203,190,57,74,76,88,207,208,239,170,
  251,67,77,51,133,69,249,2,127,80,60,159,168,81,163,64,143,146,157,56,245,
  188,182,218,33,16,255,243,210,205,12,19,236,95,151,68,23,196,167,126,61,
  100,93,25,115,96,129,79,220,34,42,144,136,70,238,184,20,222,94,11,219,224,
  50,58,10,73,6,36,92,194,211,172,98,145,149,228,121,231,200,55,109,141,213,
  78,169,108,86,244,234,101,122,174,8,186,120,37,46,28,166,180,198,232,221,
  116,31,75,189,139,138,112,62,181,102,72,3,246,14,97,53,87,185,134,193,29,
  158,225,248,152,17,105,217,142,148,155,30,135,233,206,85,40,223,140,161,
  137,13,191,230,66,104,65,153,45,15,176,84,187,22};

BYTE AES_ShiftRowTab[] = {0,5,10,15,4,9,14,3,8,13,2,7,12,1,6,11};

BYTE AES_Sbox_Inv[256];
BYTE AES_ShiftRowTab_Inv[16];
BYTE AES_xtime[256];

void AES_SubBytes(BYTE state[], BYTE sbox[]) {
  int i;
  for(i = 0; i < 16; i++)
    state[i] = sbox[state[i]];
}

void AES_AddRoundKey(BYTE state[], BYTE rkey[]) {
  int i;
  for(i = 0; i < 16; i++)
    state[i] ^= rkey[i];
}

void AES_ShiftRows(BYTE state[], BYTE shifttab[]) {
  BYTE h[16];
  memcpy(h, state, 16);
  int i;
  for(i = 0; i < 16; i++)
    state[i] = h[shifttab[i]];
}

void AES_MixColumns(BYTE state[]) {
  int i;
  for(i = 0; i < 16; i += 4) {
    BYTE s0 = state[i + 0], s1 = state[i + 1];
    BYTE s2 = state[i + 2], s3 = state[i + 3];
    BYTE h = s0 ^ s1 ^ s2 ^ s3;
    state[i + 0] ^= h ^ AES_xtime[s0 ^ s1];
    state[i + 1] ^= h ^ AES_xtime[s1 ^ s2];
    state[i + 2] ^= h ^ AES_xtime[s2 ^ s3];
    state[i + 3] ^= h ^ AES_xtime[s3 ^ s0];
  }
}

void AES_MixColumns_Inv(BYTE state[]) {
  int i;
  for(i = 0; i < 16; i += 4) {
    BYTE s0 = state[i + 0], s1 = state[i + 1];
    BYTE s2 = state[i + 2], s3 = state[i + 3];
    BYTE h = s0 ^ s1 ^ s2 ^ s3;
    BYTE xh = AES_xtime[h];
    BYTE h1 = AES_xtime[AES_xtime[xh ^ s0 ^ s2]] ^ h;
    BYTE h2 = AES_xtime[AES_xtime[xh ^ s1 ^ s3]] ^ h;
    state[i + 0] ^= h1 ^ AES_xtime[s0 ^ s1];
    state[i + 1] ^= h2 ^ AES_xtime[s1 ^ s2];
    state[i + 2] ^= h1 ^ AES_xtime[s2 ^ s3];
    state[i + 3] ^= h2 ^ AES_xtime[s3 ^ s0];
  }
}

// AES_Init: initialize the tables needed at runtime. 
// Call this function before the (first) key expansion.
void AES_Init() {
  int i;
  for(i = 0; i < 256; i++)
    AES_Sbox_Inv[AES_Sbox[i]] = i;
  
  for(i = 0; i < 16; i++)
    AES_ShiftRowTab_Inv[AES_ShiftRowTab[i]] = i;

  for(i = 0; i < 128; i++) {
    AES_xtime[i] = i << 1;
    AES_xtime[128 + i] = (i << 1) ^ 0x1b;
  }
}

// AES_Done: release memory reserved by AES_Init. 
// Call this function after the last encryption/decryption operation.
void AES_Done() {}

/* AES_ExpandKey: expand a cipher key. Depending on the desired encryption 
   strength of 128, 192 or 256 bits 'key' has to be a byte array of length 
   16, 24 or 32, respectively. The key expansion is done "in place", meaning 
   that the array 'key' is modified.
*/   
int AES_ExpandKey(BYTE key[], int keyLen) {
  int kl = keyLen, ks, Rcon = 1, i, j;
  BYTE temp[4], temp2[4];
  switch (kl) {
    case 16: ks = 16 * (10 + 1); break;
    case 24: ks = 16 * (12 + 1); break;
    case 32: ks = 16 * (14 + 1); break;
    default: 
      printf("AES_ExpandKey: Only key lengths of 16, 24 or 32 bytes allowed!");
  }
  for(i = kl; i < ks; i += 4) {
    memcpy(temp, &key[i-4], 4);
    if (i % kl == 0) {
      temp2[0] = AES_Sbox[temp[1]] ^ Rcon;
      temp2[1] = AES_Sbox[temp[2]];
      temp2[2] = AES_Sbox[temp[3]];
      temp2[3] = AES_Sbox[temp[0]];
      memcpy(temp, temp2, 4);
      if ((Rcon <<= 1) >= 256)
        Rcon ^= 0x11b;
    }
    else if ((kl > 24) && (i % kl == 16)) {
      temp2[0] = AES_Sbox[temp[0]];
      temp2[1] = AES_Sbox[temp[1]];
      temp2[2] = AES_Sbox[temp[2]];
      temp2[3] = AES_Sbox[temp[3]];
      memcpy(temp, temp2, 4);
    }
    for(j = 0; j < 4; j++)
      key[i + j] = key[i + j - kl] ^ temp[j];
  }
  return ks;
}

// AES_Encrypt: encrypt the 16 byte array 'block' with the previously expanded key 'key'.
void AES_Encrypt(BYTE block[], BYTE key[], int keyLen) {
  int l = keyLen, i;
  printBytes(block, 16);
  AES_AddRoundKey(block, &key[0]);
  for(i = 16; i < l - 16; i += 16) {
    AES_SubBytes(block, AES_Sbox);
    AES_ShiftRows(block, AES_ShiftRowTab);
    AES_MixColumns(block);
    AES_AddRoundKey(block, &key[i]);
  }
  AES_SubBytes(block, AES_Sbox);
  AES_ShiftRows(block, AES_ShiftRowTab);
  AES_AddRoundKey(block, &key[i]);
}

// AES_Decrypt: decrypt the 16 byte array 'block' with the previously expanded key 'key'.
void AES_Decrypt(BYTE block[], BYTE key[], int keyLen) {
  int l = keyLen, i;
  AES_AddRoundKey(block, &key[l - 16]);
  AES_ShiftRows(block, AES_ShiftRowTab_Inv);
  AES_SubBytes(block, AES_Sbox_Inv);
  for(i = l - 32; i >= 16; i -= 16) {
    AES_AddRoundKey(block, &key[i]);
    AES_MixColumns_Inv(block);
    AES_ShiftRows(block, AES_ShiftRowTab_Inv);
    AES_SubBytes(block, AES_Sbox_Inv);
  }
  AES_AddRoundKey(block, &key[0]);
}

// ===================== test ============================================
int main() {
  int i;
  AES_Init();
  
  BYTE block[16];
  for(i = 0; i < 16; i++)
    block[i] = 0x11 * i;

  printf("原始訊息："); printBytes(block, 16);
  
  BYTE key[16 * (14 + 1)];
  int keyLen = 32, maxKeyLen=16 * (14 + 1), blockLen = 16;
  for(i = 0; i < keyLen; i++)
    key[i] = i;

  printf("原始金鑰："); printBytes(key, keyLen);

  int expandKeyLen = AES_ExpandKey(key, keyLen);

  printf("展開金鑰："); printBytes(key, expandKeyLen);

  AES_Encrypt(block, key, expandKeyLen);

  printf("加密完後："); printBytes(block, blockLen);

  AES_Decrypt(block, key, expandKeyLen);

  printf("解密完後："); printBytes(block, blockLen);

  AES_Done();
}

執行結果

D:\Dropbox\Public\web\c\code>gcc AES.c -o AES

D:\Dropbox\Public\web\c\code>AES
原始訊息：0 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255
原始金鑰：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
 27 28 29 30 31
展開金鑰：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
 27 28 29 30 31 165 115 194 159 161 118 196 152 169 127 206 147 165 114 192 156
22 81 168 205 2 68 190 218 26 93 164 193 6 64 186 222 174 135 223 240 15 241 27
104 166 142 213 251 3 252 21 103 109 225 241 72 111 165 79 146 117 248 235 83 11
5 184 81 141 198 86 130 127 201 167 153 23 111 41 76 236 108 213 89 139 61 226 5
8 117 82 71 117 231 39 191 158 180 84 7 207 57 11 220 144 95 194 123 9 72 173 82
 69 164 193 135 28 47 69 245 166 96 23 178 211 135 48 13 77 51 100 10 130 10 124
 207 247 28 190 180 254 84 19 230 187 240 210 97 167 223 240 26 250 254 231 168
41 121 215 165 100 74 179 175 230 64 37 65 254 113 155 245 0 37 136 19 187 213 9
0 114 28 10 78 90 102 153 169 242 79 224 126 87 43 170 205 248 205 234 36 252 12
1 204 191 9 121 233 55 26 194 60 109 104 222 54
0 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255
加密完後：142 162 183 202 81 103 69 191 234 252 73 144 75 73 96 137
解密完後：0 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255

您可以看到在「原始訊息」與「解密完後」的內容是一樣的，這代表加密再解密後可以完全環原整個訊息，因此程式的運作是正確的。

結語

在本文中，我們看到了一個相當先進的 AES 加解密方法，雖然我們對每個程式步驟的做法都看得很清楚，但是整個系統的原理卻仍然令人感到神秘，因為裡面有不少數學理論存在，特別是有關數論的理論。

不過、相信各位程式人應該可以透過這個程式，感受到現代加解密系統的奧秘，如果讀者還有興趣的話，或許可以從以下參考文獻當中，進一部瞭解 AES 的數學原理。

說明：本文的圖片來自維基百科，由於這幾幅圖片乃是用「公共領域授權」的方式釋出，因此本文可以合法的使用，而且不需要採用維基百科的「創作共用」授權釋出。

參考文獻

  1. jsaes: AES in JavaScript
  2. Wikipedia:Advanced_Encryption_Standard
  3. 維基百科：高階加密標準

後續 >> RSA 非對稱型加解密演算法 – 使用 C 語言實作

分享：
按讚！加入 CodeData Facebook 粉絲群

留言

留言請先。還沒帳號註冊也可以使用Facebook、Google+登錄留言

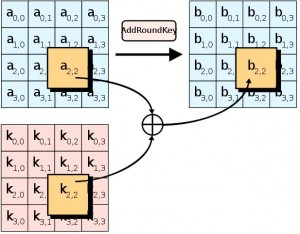
snaku07/05

好文章，感謝您的分享

關於作者

陳鍾誠

Email Facebook GitHub

職務：國立金門大學 / 資訊工程系 / 助理教授 首頁：http://ccckmit.wikidot.com/

熱門論壇文章

熱門技術文章