Haskell Tutorial（30）解決巢狀結構的 Monad << 前情

在〈Haskell Tutorial（30）解決巢狀結構的 Monad〉最後說到，do 與 <- 綁定 其實是可以用在 Monad 上，而不只是 IO，這邊就實際來看看，像 Maybe、List 可以如何與 do 及 <- 一起使用。

Maybe、do 與 <-

假設你從某個運算取得了 maybeName::Maybe String，又從另一個運算取得了 maybeBirth::Maybe Int，現在打算將它們進行串接，取得一個字串，你會怎麼做？如果使用模式比對，你得判斷是不是有值，你可能會想到 Maybe Applicative，它已經實作了有無值的判斷，這是個好主意！你可以使用 (++) <$> something <*> (show <$> another) 來得到想要的結果。

不過，你有更好的做法：

account :: Maybe String -> Maybe Int -> Maybe String
account maybeName maybeBirth = do
    name <- maybeName
    birth <- maybeBirth
    return (name ++ (show birth))

這麼一來，你就可以如此使用：

如果使用 do 區塊與 <- 綁定，你就得寫出一串 Lambda：

account :: Maybe String -> Maybe Int -> Maybe String
account maybeName maybeBirth =
    maybeName >>= (\name ->
    maybeBirth >>= (\birth ->    
    return (name ++ (show birth))))

這也說明了，為什麼 do 區塊最後不能是 <- 綁定，想想看，如果 do 區塊最後 <- 綁定，那這個 Lambda 怎麼寫呢？

List、do 與 <-

將一開始的 account 函式型態宣告拿掉，也就是只寫為：

account mName mBirth = do
    name <- mName
    birth <- mBirth
    return (name ++ (show birth))

由編譯器為你判定型態，你覺得結果會怎樣？

實際上，account 只用到了 Monad 定義的 return 方法，判斷為 (Monad m, Show a) => m [Char] -> m a -> m [Char] 是最寬鬆的結果，如此一來，account 不僅可適用 Maybe，也可以適用 List，就像上面示範的，給 account 的 List 只有一個元素時很好理解，就是將唯一的元素綁定到名稱上，如果給 account 的 List 不只有一個元素時會如何呢？

難以理解嗎？重新看看不用 do 時會怎麼寫，就應該能知道為什麼對 List 做 do 與 <-，會有這樣的結果：

account mName mBirth =
    mName >>= (\name ->
    mBirth >>= (\birth ->    
    return (name ++ (show birth))))

我們對 mName 套用 >>=，記得嗎？List 在實作 >>= 的方式是 concat (fmap f xs)，也就是說對 mName 套用 >>=，結果就是 concat (fmap f mName)，如果 mName 實際上超過一個元素，就會逐一取得並套用 f 後串接起來，後 f 是個 Lambda，它對 mBirth 套用 >>=，如果 mBrith 實際上超過一個元素，就會逐一取得並套用 f 後串接起來，最後就得到與 [name ++ (show birth) | name <- ["Justin", "Monica"], birth <- [526, 723]] 這個 List Comprehension 相同的結果。

將以下函式與上頭的函式對照一下，你就更容易記得，對 List 使用 do 與 <- 會是什麼結果了：

account mName mBirth = 
    [name ++ (show birth) | 
     name  <- mName, 
     birth <- mBirth]

也就是說，對 List 使用 do 與 <- 時，將 <- 想成是 List Comprehension 的 <- 就是了，實際上，List Comprehension 是個語法蜜糖，跟使用 do 一樣，List Comprehension 最後也是使用 >>= 來進行運算。

回顧一下自訂迴圈

方才看而，一開始的 account 函式可以讓編譯器自動推斷為 (Monad m, Show a) => m [Char] -> m a -> m [Char]，因此，account 也可以適用 IO：

這讓我們想起來，在〈Haskell Tutorial（21）來寫些迴圈吧！〉中提到，Haskell 的 Control.Monad 中有些函式，實際上並不只能用在 IO，像 forM 型態是 Monad m => [a] -> (a -> m b) -> m [b]，除了使用在 IO，你也可以使用在 Maybe 或 List：

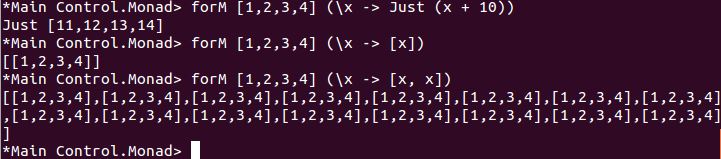
嗯？最後的顯示結果為什麼會這樣，你可以根據〈〈Haskell Tutorial（21）來寫些迴圈吧！〉最後的題目實作成果，將 sequence'、forM' 修改為支援 Monad 版本，就知道為什麼了！

後續 >> Haskell Tutorial（32）發掘具有組合性的行為